By

问题描述

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

https://leetcode.com/problems/longest-palindromic-substring/

DP解法

注意回文串有两种形式：a和aa，也就是中轴是一个元素或者两个元素。
可以转化为求解s和s逆序（例如dabcbaee和eeabcbad）的最长公共子串，并且这两个子串在原串中是相邻的，（例如abcjiecba中，abc和cba虽然最长公共子串，但并不相邻）

dp[i][j]表示以s以i结尾，s逆序(s’)以j结尾的两个字符串的最长公共子串的长度。可以得到递推式：
dp[i][j] = dp[i-1][j-1] + 1 (if s[i]===s’[j])
dp[i][j] = 0 (if s[i] !== s’[j])

判断相邻的条件：(i + j - dp[i][j] + 1 === len) || (i + j - dp[i][j] === len)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
var longestPalindrome = function(s) {
    var len = s.length, max=0, end;
	var dp = [];
	for (var i=0; i<=len; i++)
	{
		dp[i] = [];
		dp[i][0] = 0;
		dp[0][i] = 0;
	}
	
	for (var i=1; i<=len; i++)
	{
		for (var j=1; j<=len; j++)
		{
			if (s[i-1] === s[len-j])
			{
				dp[i][j] = dp[i-1][j-1] + 1;
				if (dp[i][j] > max)
				{
				    if ((i + j - dp[i][j] + 1 === len) || (i + j - dp[i][j] === len))
					{
						max=dp[i][j];
						end = i;
					}
				}
			}
			else
			{
				dp[i][j] = 0;
			}
		}
	}
	
	return s.substring(end - max, end);
};

这个算法的时间复杂度为O(n^2),空间复杂度为O(n^2)。后面的Manacher算法可以将时间和空间复杂度降低为O(n)。

Manacher算法

例子：dabcbaee

1.加入#
目的：这样可以简化问题，把aaa和aaaa这两种类型的回文串，变为同一种以单一元素为轴的对称。

#d#a#b#c#b#a#e#e#

2.计算可以扩展长度的向量

#d#a#b#c#b#a#e#e#
[1, 2, 1, 2, 1, 2, 1, 6, 1, 2, 1, 2, 1, 2, 3, 2, 1]

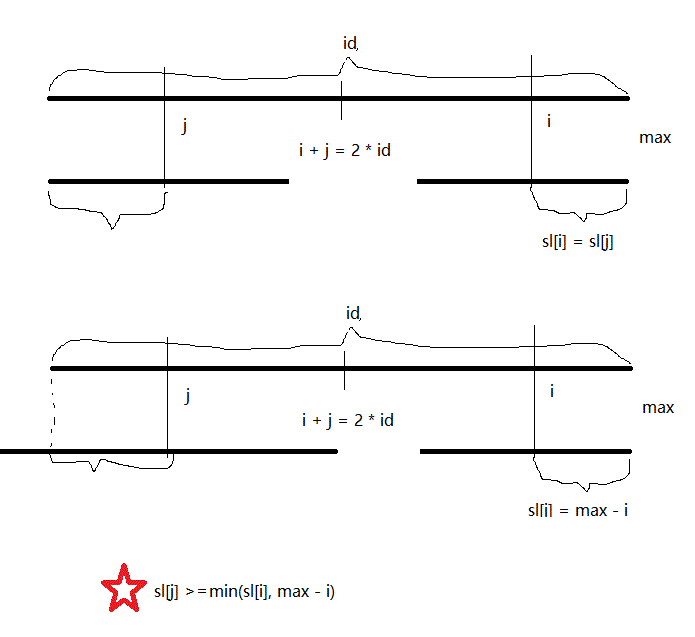
3.计算时候可以利用回文串的性质进行优化

palindromic string property makes its big O to O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
var longestPalindrome = function(s) {
    var s2 = '#';
	for (var i=0; i<s.length; i++)
	{
		s2 += s[i] + '#';
	}
	
	var sl = [1], max = 0, id = 0, maxid = 0;
	for (var i = 1; i < s2.length; i++)
	{
		var cnt = 1;
		if(i < max)
		{
			var pilot = id * 2 - i;
			cnt = sl[pilot] < max - i + 1 ? sl[pilot] : max - i + 1;
		}
		
		var tp=i-cnt, tn=i+cnt;		
		while(tp >= 0 && tn < s2.length && s2[tp] === s2[tn])
		{
			cnt ++;
			tp --;
			tn ++;
		}
		
		sl[i] = cnt;
		if (i + cnt - 1 > max)
		{
			max = i + cnt - 1;
			id = i;
			if (sl[i] > sl[maxid])
			{
				maxid = i;
			}
		}
	}
	
	var start = Math.floor((maxid - sl[maxid] + 1) / 2);
	return s.substring(start, start + sl[maxid] - 1);
};