从矩阵左上角至右下角（无权值）问题

Contents

1. 1. 问题来源
2. 2. 问题描述
3. 3. 问题解法
   1. 3.1. 数学解法
   2. 3.2. 递归解法
   3. 3.3. 动态规划解法

问题来源

来自于Euler Project的第十五个题目，题目不复杂，但是可以有很多种思路和解法。此外，我宿舍一姐们面试刚好碰到此题。题目链接

问题描述

一个 M*N 的矩阵，从矩阵的左上角到矩阵的右下角，只能向右走或者向下走，有多少种解法？

例如一个2*2的矩阵，有下面六种解法。

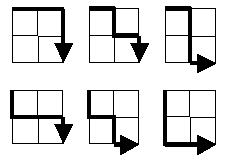
问题解法

假设矩阵有M行N列。

数学解法

使用排列组合有两种思路。因为只能向右走或者向下走。

（1）在M+N次行走后，才能到达终点，也就是右下角，而在这M+N次行走中，有M次是向下，N次向右。所以是一个选择问题。

$$ {C_{m+n}^{m}} \tag{1} $$

对于Euler这题而言，就是C(40, 20)，在google中输入40 choose 20，答案就出来啦。

（2）水平行走记作0，竖直行走记作1。每一种行走足迹可以作为一个0,1串，其中n个0，m个1。可以看做0000000000000（n个0）1111111111111（m个1）的重排列。

也就是

$$ \frac{(m+n)!}{m!n!} \tag{2} $$

如果实在想不出公式，可以写出前面一些特殊的然后找规律，这也是没有办法的办法了，但是不一定有效。

递归解法

递归，动态规划，说白了，就是把一个问题分解成子问题，然后找出最小子问题。动态规划还需要找出问题的求解顺序。

因此，我们发现了这个问题的递归式：

matrix[i][j]=matrix[i-1][j] + matrix[i][j-1]
初始条件：matrix[i][0]=matrix[0][j]=1

#include <stdio.h>  
#include <stdlib.h>  
#include <time.h>  
__int64 digui(int row, int col){  
        if(row == 1 || col == 1) return 1;  
        else return digui(row-1, col) + digui(row, col-1);  
}  
int main(){  
    clock_t begin = clock();  
    printf("%lld\n", digui(18,18));  
    clock_t end = clock();  
    double cost = (double)(end - begin) / CLOCKS_PER_SEC;  
    printf("%lf seconds\n", cost);  
    system("pause");  
}  

但是，递归因为不记录中间结果，会重复计算很多中间值，超级费时！
比如这个程序在我的PC上跑，1616的时候，需要3.727000秒。而1717规模，需要13.601000秒，当问题规模到1818时候计算时间已经到了52.803000秒了，基本到2121是很慢很慢的了。

动态规划解法

和递归的原理差不多，需要多注意一个问题就是计算顺序的问题。这个题就按顺序一行一行扫描就行了。

#include<stdio.h>  
#define XMAX 21  
#define YMAX 21  
int main() {  
  __int64 matrix[XMAX][YMAX];  
  for(int i=0;i<XMAX;i++) matrix[i][0]=1;  
  for(int i=0;i<YMAX;i++) matrix[0][i]=1;  
  for(int i=1;i<XMAX;i++)   
    for(int j=1;j<YMAX;j++)  
      matrix[i][j]=matrix[i-1][j]+matrix[i][j-1];  
  printf("%lld",matrix[20][20]);  
}